¶ 题目0245-信号发射和接收
¶ 题目描述
有一个二维的天线矩阵,每根天线可以向其他天线发射信号,也能接收其他天线的信号,为了简化起见,我们约定每根天线只能向东和向南发射信号,换言之,每根天线只能接收东向或南向的信号。
每根天线有自己的高度anth,每根天线的高度存储在一个二维数组中,各个天线的位置用[r, c]表示,r代表天线的行位置(从0开始编号),c代表天线的列位置(从0开始编号)。
在某一方向(东向或南向),某根天线可以收到多根其他天线的信号(也可能收不到任何其他天线的信号),对任一天线X和天线Y,天线X能接收到天线Y的条件是:
天线X在天线Y的东边或南边
天线X和天线Y之间的其他天线的高度都低于天线X和天线Y,或天线X和天线Y之间无其他天线,即无遮挡。
如下图示意:
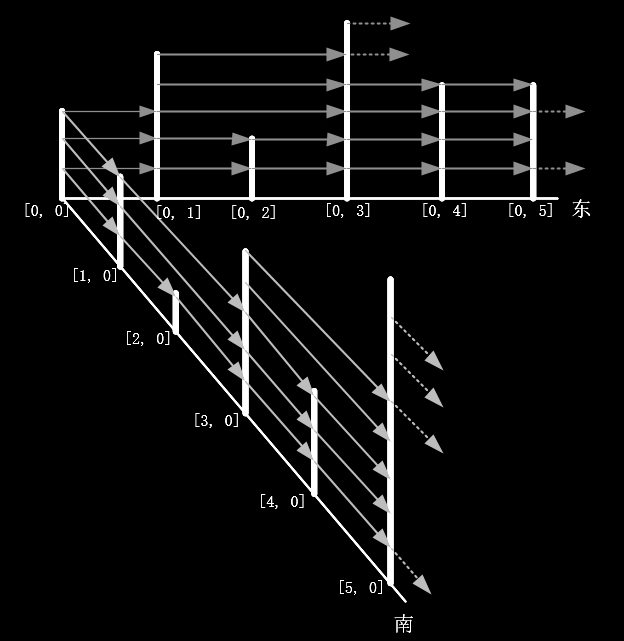
在天线矩阵的第0行上:
- 天线
[0, 0]接收不到任何其他天线的信号, - 天线
[0, 1]可以接收到天线[0, 0]的信号, - 天线
[0, 2]可以接收到天线[0, 1]的信号, - 天线
[0, 3]可以接收到天线[0, 1]和天线[0, 2]的信号, - 天线
[0, 4]可以接收到天线[0, 3]的信号, - 天线
[0, 5]可以接收到天线[0, 4]的信号;
在天线的第0列上:
- 天线
[0, 0]接收不到任何其他天线的信号, - 天线
[1, 0]可以接收到天线[0, 0]的信号, - 天线
[2, 0]可以接收到天线[1, 0]的信号, - 天线
[3, 0]可以接收到天线[1, 0]和天线[2, 0]的信号, - 天线
[4, 0]可以接收到天线[3, 0]的信号, - 天线
[5, 0]可以接收到天线[3, 0]和天线[4, 0]的信号;
给一个m行n列的矩阵(二维数组),矩阵存储各根天线的高度,求出每根天线可以接收到多少根其他天线的信号,结果输出到m行n列的矩阵(二维矩阵)中。
¶ 输入描述
输入为1个m行n列的矩阵(二维矩阵)anth[m][n],矩阵存储各根天线的高度,高度值anth[r]][c]为大于0的整数。
第一行为输入矩阵的行数和列数,如:
m n
第二行为输入矩阵的元素值,按行输入,如:
anth[0][0] anth[0][1] ... anth[0][n-1] anth[1][0] anth[1][1] ... anth[1][n-1] ... anth[m-1][0] ... anth[m-1][n-1]
¶ 输出描述
输出一个m行n列的矩阵(二维数组)ret[m][n],矩阵存储每根天线能收到多少根其他天线的信号,根数为ret[r][c]。
第一行为输出矩阵的行数和列数,如:
m n
第二行为输出矩阵的元素值,按行输出,如:
ret[0][0] ret[0][1] ... ret[0][n-1] ret[1][0] ret[1][1] ... ret[1][n-1] ... ret[m-1][0] ... ret[m-1][n-1]
¶ 备注
¶ 示例一
¶ 输入
1 6
2 4 1 5 3 3
¶ 输出
1 6
0 1 1 2 1 1
¶ 说明
输入为1行6列的天线矩阵的高度值
[2 4 1 5 3 3]
输出为1行6列的结果矩阵
[0 1 1 2 1 1]
¶ 示例二
¶ 输入
2 6
2 5 4 3 2 8 9 7 5 10 10 3
¶ 输出
2 6
0 1 1 1 1 4 1 2 2 4 2 2
¶ 说明
输入为2行6列的天线矩阵高度值
[2 5 4 3 2 8]
[9 7 5 10 10 3]
输出为2行6列的结果矩阵
[0 1 1 1 1 4]
[1 2 2 4 2 2]
¶ 思路解析和复杂度分析
这道题目要求从一个二维矩阵(代表天线的高度)中计算出每个天线能接收到多少个其他天线的信号。每个天线只能向东(即向右)或向南(即向下)接收信号,而且必须满足天线X和天线Y之间的所有天线的高度都低于天线X和天线Y。所以,我们需要对每个天线进行检查,看它能否接收到其他天线的信号。
¶ 思路解析:
-
我们从右下角开始反向遍历这个二维矩阵。对于每个天线,我们都检查它的右边和下边的天线,看它们的高度是否低于当前天线。如果是,那么就说明当前天线可以接收到这个天线的信号。
-
对于向右(东向)的检查,我们从当前天线的右边一直检查到最右边的天线。如果某个天线的高度低于当前天线,那么就增加当前天线的接收信号数。如果某个天线的高度高于或等于当前天线,那么就停止检查。
-
对于向下(南向)的检查,同样是从当前天线的下边一直检查到最下边的天线。如果某个天线的高度低于当前天线,那么就增加当前天线的接收信号数。如果某个天线的高度高于或等于当前天线,那么就停止检查。
-
在检查过程中,我们需要保存每个天线的接收信号数。这可以通过创建一个和输入矩阵同样大小的二维矩阵来实现。每当一个天线的接收信号数增加时,就在对应位置的矩阵元素上加1。
¶ 复杂度分析:
-
时间复杂度:O(mn(m+n))。这是因为我们对每个天线都进行了两次遍历,一次向右,一次向下。每次遍历的时间复杂度是O(m+n)。因为矩阵的大小为mn,所以总的时间复杂度是O(mn*(m+n))。
-
空间复杂度:O(mn)。这是因为我们需要保存输入矩阵和结果矩阵,它们的大小都是mn。因此,总的空间复杂度是O(m*n)。
需要注意的是,这个解法在天线矩阵较大时可能会比较慢。如果需要更快的解法,可能需要使用一些更复杂的数据结构和算法,比如使用栈(stack)或者线段树(segment tree)来更快地找出每个天线能接收到的信号数。
¶ 参考解题
¶ 参考解题 C
#include <stdio.h>
#include <string.h>
#define MAX 500
int anth[MAX][MAX];
int ret[MAX][MAX];
int main() {
int m, n;
scanf("%d %d", &m, &n);
// 读取输入矩阵
for(int i=0; i<m; i++) {
for(int j=0; j<n; j++) {
scanf("%d", &anth[i][j]);
}
}
// 初始化结果矩阵为0
memset(ret, 0, sizeof(ret));
// 从右下角开始反向遍历
for(int i=m-1; i>=0; i--) {
for(int j=n-1; j>=0; j--) {
if(i != m-1) {
// 检查南向的信号
int k = i + 1;
while(k < m && anth[k][j] < anth[i][j]) {
ret[i][j]++;
k++;
}
}
if(j != n-1) {
// 检查东向的信号
int k = j + 1;
while(k < n && anth[i][k] < anth[i][j]) {
ret[i][j]++;
k++;
}
}
}
}
// 输出结果矩阵
printf("%d %d\n", m, n);
for(int i=0; i<m; i++) {
for(int j=0; j<n; j++) {
printf("%d ", ret[i][j]);
}
printf("\n");
}
return 0;
}
¶ 参考解题 C++
#include <iostream>
#include <vector>
using namespace std;
#define MAX 500
vector<vector<int>> anth(MAX, vector<int>(MAX, 0));
vector<vector<int>> ret(MAX, vector<int>(MAX, 0));
int main() {
int m, n;
cin >> m >> n;
// 读取输入矩阵
for(int i=0; i<m; i++) {
for(int j=0; j<n; j++) {
cin >> anth[i][j];
}
}
// 从右下角开始反向遍历
for(int i=m-1; i>=0; i--) {
for(int j=n-1; j>=0; j--) {
if(i != m-1) {
// 检查南向的信号
int k = i + 1;
while(k < m && anth[k][j] < anth[i][j]) {
ret[i][j]++;
k++;
}
}
if(j != n-1) {
// 检查东向的信号
int k = j + 1;
while(k < n && anth[i][k] < anth[i][j]) {
ret[i][j]++;
k++;
}
}
}
}
// 输出结果矩阵
cout << m << " " << n << "\n";
for(int i=0; i<m; i++) {
for(int j=0; j<n; j++) {
cout << ret[i][j] << " ";
}
cout << "\n";
}
return 0;
}
¶ 参考解题 Java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 读取矩阵行列数
int m = scanner.nextInt();
int n = scanner.nextInt();
// 初始化矩阵
int[][] anth = new int[m][n];
int[][] ret = new int[m][n];
// 读取输入矩阵
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
anth[i][j] = scanner.nextInt();
}
}
// 从右下角开始反向遍历
for(int i = m-1; i >= 0; i--) {
for(int j = n-1; j >= 0; j--) {
if(i != m-1) {
// 检查南向的信号
int k = i + 1;
while(k < m && anth[k][j] < anth[i][j]) {
ret[i][j]++;
k++;
}
}
if(j != n-1) {
// 检查东向的信号
int k = j + 1;
while(k < n && anth[i][k] < anth[i][j]) {
ret[i][j]++;
k++;
}
}
}
}
// 输出结果矩阵
System.out.println(m + " " + n);
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
System.out.print(ret[i][j] + " ");
}
System.out.println();
}
scanner.close();
}
}
¶ 参考解题 Python
def calculate_signal():
# 读取矩阵的行列数
m, n = map(int, input().split())
# 初始化矩阵
anth = [[0]*n for _ in range(m)]
ret = [[0]*n for _ in range(m)]
# 读取输入矩阵
for i in range(m):
anth[i] = list(map(int, input().split()))
# 从右下角开始反向遍历
for i in range(m-1, -1, -1):
for j in range(n-1, -1, -1):
if i != m-1:
# 检查南向的信号
k = i + 1
while k < m and anth[k][j] < anth[i][j]:
ret[i][j] += 1
k += 1
if j != n-1:
# 检查东向的信号
k = j + 1
while k < n and anth[i][k] < anth[i][j]:
ret[i][j] += 1
k += 1
# 输出结果矩阵
print(m, n)
for row in ret:
print(' '.join(map(str, row)))
if __name__ == '__main__':
calculate_signal()
¶ 参考解题 JavaScript
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
terminal: false
});
let lines = [];
rl.on('line', (line) => {
lines.push(line);
});
rl.on('close', () => {
const [m, n] = lines[0].split(' ').map(Number);
let anth = new Array(m).fill(0).map(() => new Array(n).fill(0));
let ret = new Array(m).fill(0).map(() => new Array(n).fill(0));
for(let i=0; i<m; i++) {
anth[i] = lines[i+1].split(' ').map(Number);
}
for(let i=m-1; i>=0; i--) {
for(let j=n-1; j>=0; j--) {
if(i != m-1) {
// 检查南向的信号
let k = i + 1;
while(k < m && anth[k][j] < anth[i][j]) {
ret[i][j]++;
k++;
}
}
if(j != n-1) {
// 检查东向的信号
let k = j + 1;
while(k < n && anth[i][k] < anth[i][j]) {
ret[i][j]++;
k++;
}
}
}
}
// 输出结果矩阵
console.log(m + ' ' + n);
for(let i=0; i<m; i++) {
console.log(ret[i].join(' '));
}
});
¶ 参考解题 Go
package main
import (
"bufio"
"fmt"
"os"
"strconv"
"strings"
)
func main() {
scanner := bufio.NewScanner(os.Stdin)
// 读取矩阵的行列数
scanner.Scan()
line := strings.Split(scanner.Text(), " ")
m, _ := strconv.Atoi(line[0])
n, _ := strconv.Atoi(line[1])
// 初始化矩阵
anth := make([][]int, m)
ret := make([][]int, m)
// 读取输入矩阵
for i := 0; i < m; i++ {
scanner.Scan()
line := strings.Split(scanner.Text(), " ")
anth[i] = make([]int, n)
ret[i] = make([]int, n)
for j := 0; j < n; j++ {
anth[i][j], _ = strconv.Atoi(line[j])
}
}
// 从右下角开始反向遍历
for i := m - 1; i >= 0; i-- {
for j := n - 1; j >= 0; j-- {
if i != m-1 {
// 检查南向的信号
k := i + 1
for k < m && anth[k][j] < anth[i][j] {
ret[i][j]++
k++
}
}
if j != n-1 {
// 检查东向的信号
k := j + 1
for k < n && anth[i][k] < anth[i][j] {
ret[i][j]++
k++
}
}
}
}
// 输出结果矩阵
fmt.Println(m, n)
for _, row := range ret {
for _, value := range row {
fmt.Printf("%d ", value)
}
fmt.Println()
}
}